チュートリアル / Psyop：Todd Akitaと歩むICEマスターへの道のり
第3回：「ICE: デザイン ツール」

基礎の習熟から

皆様、お久しぶりです。前回からしばらくお時間が経ってしまったので、今回のコラムからは、あらためて基礎の習熟についての解説をしばらく行なっていこうと思います。

日々利用しているグラフィックスツールを制御する数学により理解を深めるために、テクニカルディレクタやテクニカルアーティストにとって最適な入り口がICEです。その使いやすさは実験を楽しいものにし、結果を素早くヴィジュアライズすることで学習もはかどることでしょう。

このコラムの内容は、2010年と2011年のマスタークラスで発表を行った「ICE：法則の応用」のセッション内容を凝縮したものです。テクニカルアーティストが数学の基礎を復習するため、あるいは日々の業務で必要とされる知識と高校時代に学んだ内容のギャップを埋めることを目標としています。

このため、なるべく簡潔な説明に主眼を置いています。後々のレッスンで登場する外積の計算では、成分ごとのソリューションが行列乗算や回転にどう作用するかといった詳細は省略されています。

一般的には、ゼロから計算する方法を学ぶよりも、どのような時にこれらの演算を使用するのかを理解するほうが重要です。計算方法の詳細については、オンラインのWikipediaやコンピュータグラフィックスの入門書籍をご覧ください。さらに深く学習したい人には、David Eberly氏の “Geometric Tools for Computer Graphics”やJohn Vince氏の“Mathematics for Computer Graphics”といった書籍がおすすめです。

三角法

ピタゴラスの定理

三角法のピタゴラスの定理は、斜辺以外の2辺の長さをもとに斜辺の長さを導き出します。
A² + B² = C² で A と B は直角三角形の斜辺以外の 2 辺（隣辺）の長さを表し、C は斜辺の長さを表します。(図：1a).



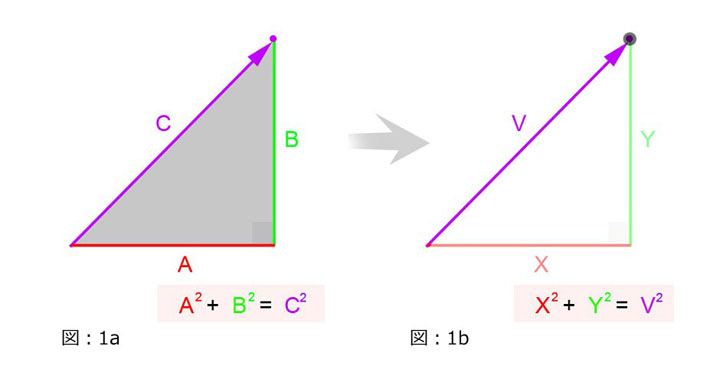
直角三角形の C辺を算出することは、2Dベクトル V を算出することと同様です。V のx と y コーディネート(V.x と V.y)は、直角三角形でいうところの隣辺です。 (図：1b)

ピタゴラスの定理は、平方根を求める前に 3 番目の要素の二乗を加えることで、2 次元 (x, y) から 3 次元 (x, y, z) に簡単に拡張できます。3D空間でのピタゴラスの定理は、A² + B² + C² = D² です。



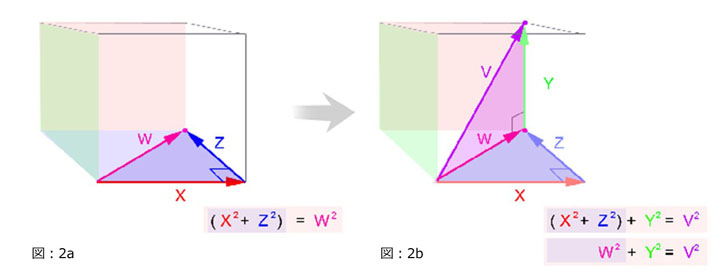
XYZコンポーネントからなる二次元の三角形を2つ組み合わせることで、3次元空間でピタゴラスの定理を視覚化することも可能です。一つ目の三角形（斜辺W）は、XZ平面上にW.x と W.z を隣辺として存在します。(図：2a)　

2つめの三角形（斜辺V）は、右奥に向かってXZ平面のW とV.y を隣辺として存在します。(図：2b)　

改めて説明を行いますが、3D空間での三角法（ピタゴラスの定理）は、2D ( A² + B² = C² )に簡素化させて考えることが可能です。なぜなら、三角形は3D空間に存在しながらも常に平面的でフラットだとも解釈できるからです。

実際にICEとして処理を考えると、三角法（あるいは、ベクトルV）で長さを求めたいと思ったときは、おそらくは(図：2c)の上図のようにA² + B² + C² = D² としてノードを構築する必要があるでしょう。



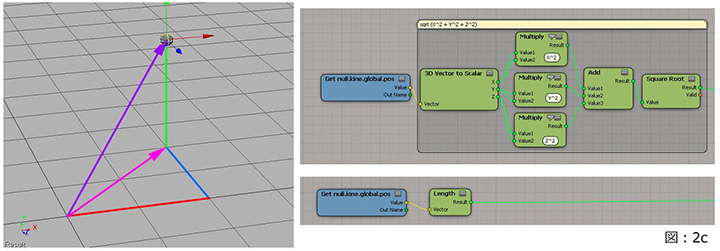
単にベクトルの長さを求めたいだけであれば、 Softimage の標準ICEノードである「Length」を利用すると良いでしょう。やはり、用意されているノードを利用するほうが何かと作業は楽に進められると思います。しかも、三角法については、標準機能でかなりカバーされていると言っても過言ではありません。

しかしながら、ICEの強みはプロジェクトの進行に伴い自分が必要とする機能をデザイン出来る事です。クリエイティブな目標に向かってサブタスクを解決していくなかで、基礎数学のノウハウを活かすことで柔軟性が得られるのです。

正弦(サイン/sine)、余弦(コサイン/cosine)、正接(タンジェント/tangent)

直角三角形の内角が分かれば、正弦(サイン/sine)、余弦(コサイン/cosine)、正接(タンジェント/tangent)関数を利用することで常に他の 2 辺の相対的に長さを求めることができます。

逆に言うと、これらの逆関数である逆正弦(アークサイン/ArcSine)、逆余弦(アークコサイン/ArcCosine)、逆正接(アークタンジェント/ArcTangent)を利用すると、2辺の長さから内角を求められます。（図：3）



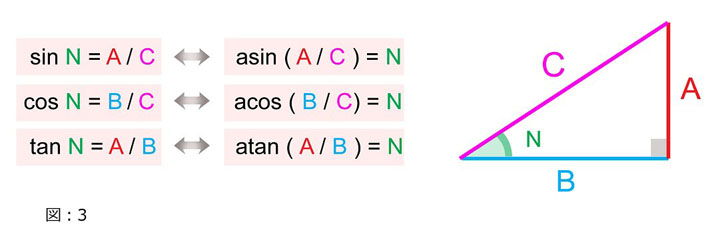
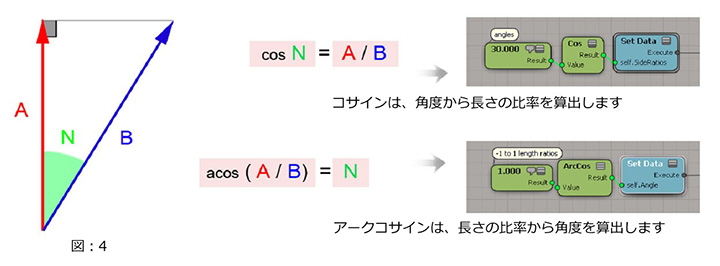
例えば、直角三角形の角度 N を与えられた場合に、その角度 N に対して余弦(コサイン/cosine) を利用することで辺 A と B の相対的な長さを求めることが出来るのです。逆に辺 A と B の長さに対して、逆余弦(アークコサイン/ArcCosine) を利用すると角度 N を導き出せるのです。（図：4）



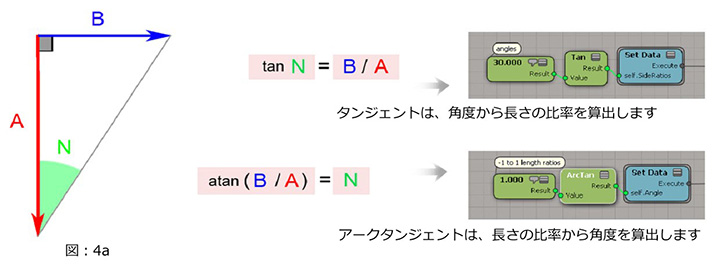
長さがわかっている辺に対しては、正しい関数を使用することが常に大事です。この場合は、異なる2辺がわかっているために、余弦(コサイン/cosine)ではなく、正接(タンジェント/tangent)関数を利用する必要があります。（図：4a）



三角法で求めたい辺に対応する関数を暗記するための英語のフレーズとして、「Soh-Cah-Toa」というものがあります。



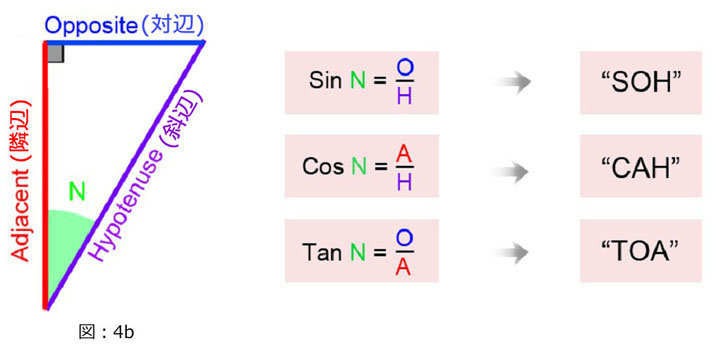
それぞれの最初のアルファベットは、三角関数の頭文字に対応しています。（例：Sine　Cosine や Tangent）そして、2辺の長さとペアになっています。 (例：Adjacent (隣辺) Opposite（対辺） Hypotenuse（斜辺）).

例:
“SOH” は、 Sine = Opposite (対辺) / Hypotenuse（斜辺）
“CAH” は、 Cosine = Adjacent (隣辺) / Hypotenuse（斜辺）
“TOA” は、 Tangent = pposite（対辺）/Adjacent (隣辺)

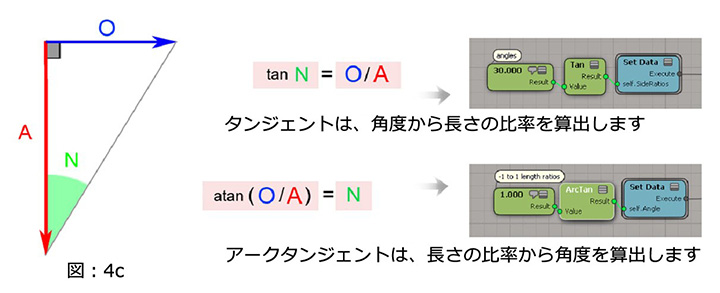
もちろん、同じ記憶法を逆関数に対して利用することも出来るでしょう。

次の例では、対辺と隣辺の長さを割り算したうえで、逆三角関数の逆正接(ArcTangent)で角度 N を導き出すことが可能です。（図：4c）



逆三角関数の実践的な利用方法は、カメラの光学焦点距離(Focal length)と撮像素子(Film-back)のサイズから水平 FOV 角度を求めるケースです。(図：5)



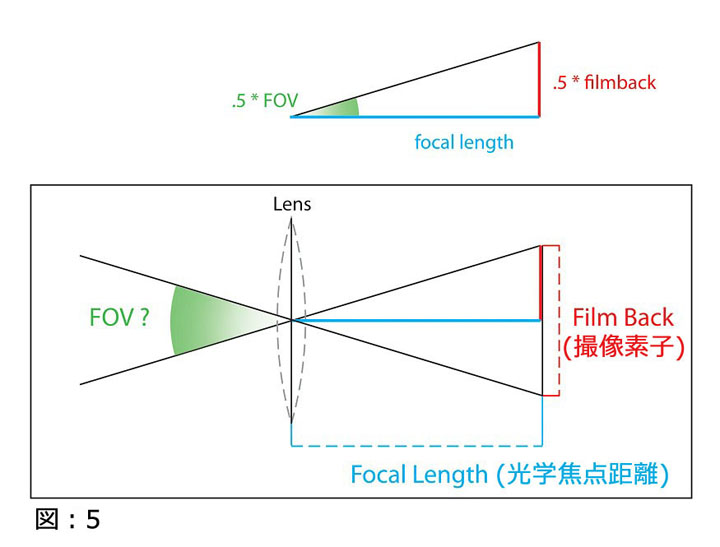
このケースでは、三角形の直角2辺(Folcal LengthとFilm-backの半分)が判明しているので、逆正接(アークタンジェント/ArcTangent)を使って FOV角度を求めるべきでしょう。三角形の内角が求められたら、その結果の角度を二倍することで適切なFOV角度が求められるのです。

方程式は次のとおりです: FOV = 2 * atan (.5 * filmback / focal_length)

次回のレッスンでは、サイン・コサインについてもう少し詳しく学んでいきたいと思います。