チュートリアル / Psyop：Todd Akitaと歩むICEマスターへの道のり
第1回：はじめてのICEモデリング - トポロジーを理解する

イントロダクション

Softimage 2012の魅力的な新機能の一つが、ICEを利用したメッシュのトポロジー編集機能です。

これまでもICEを利用することで大量のパーティクルを制御したり、重たいメッシュを変形させたりといったことが可能でした。しかし、このようなポイントクラウドやパーティクルに対する高度な制御をポリゴンメッシュに対しても同様に行なうことは、2012の登場までは夢の話でした。

つまり、ICEで既存メッシュの形状やプロパティを変更したりすることは出来ても、新規にメッシュを生成したり、既存メッシュの頂点、エッジ、ポリゴン面を削除や追加することはできなかったのです。

ICEでトポロジーにアクセス出来るようになったことで、ICEを利用してメッシュを動的に生成させることが可能になりました。プロシージャルモデリングや生成的デザインの実現、アーティスト自身も機能開発が可能な環境というのは、次世代のアーティストツールにとっては大きな武器と言えます。アート制作の課程で機能自体も開発してしまおうと考えるのも自然な流れと言えます。

Softimage 2012にはメッシュトポロジーを生成するための便利なコンパウンドがたくさん搭載されています。今回の記事を通じてゼロの状態からポリゴンを生成するまでの基礎知識をご紹介したいと考えています。
最終的には、さらに複雑なタスクについても解説したいと考えています。しかし、まずはベースとなる基礎知識を身につけるところからスタートをしたいと思います。

トポロジーとは？

トポロジーは、空間や位置の研究で用いられる単語です。頂点間の関係性を描くことで、頂点だけでなくその間にある空間も描く仕組みです。

ポイントクラウドとポリゴンメッシュの違いを想像してみてください。例えば、ポイントクラウドとポリゴンメッシュの両方ともにポイントの集合から形成されています。しかし、ポリゴンメッシュがポイントクラウドと異なる点として、頂点だけでなく頂点の関係性を描く構造情報を持っていることです。


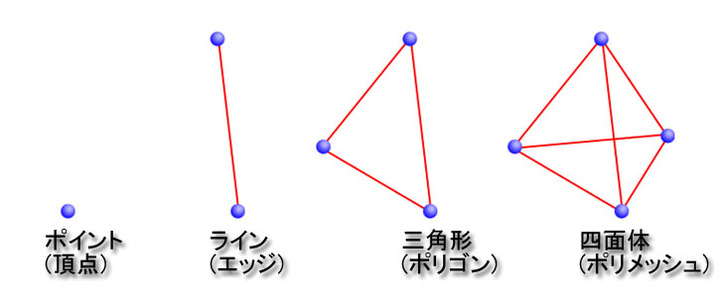
頂点(vertex)はポイントによって定義されますが、もっと具体的に言うとポリゴンメッシュと関係性を持つポイントです。2つの頂点の接続情報は、長さを持つエッジを形成します。そして、3つ以上のエッジでポリゴンの境界線が定義されます。ポリゴンの集合がポリゴンメッシュと呼ばれるボリュームを持ちうるオブジェクトを形成するのです。

このため、ポリゴンメッシュを別の見方をすると構造化されたポイントクラウドとも言えます。その構造がメッシュの特徴を定義し、メッシュのトポロジーと構造をみなすことが可能なのです。

ここで鍵となる考えは、これら構造の関係性はメッシュの特徴を定義することです。トポロジーの概念は、実際のポイント自体とそのコンポーネントの間に存在する関係性であるとみなされるのです。

プランの考察

ICEトポロジーオペレータのルールの一つに、オブジェクトのオペレータスタックとしてモデリングのコンストラクションモードでのみ有効であることが挙げられます。これは、従来からのモデリング機能オペレータのルールを踏襲しています。このため、ルールにしたがってプランを建てましょう。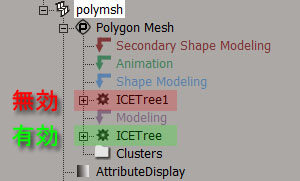

手始めに

ICEでメッシュを作成するためには、"Create Topo"ICEノードからの結果を"Set Topology"ノードに接続します。下図の例では単一の三角形ポリゴンを作成しています。

"Create Topo"ノードでは、2つの情報を必要とします。頂点の位置情報、そして、これら頂点の接続順番です。



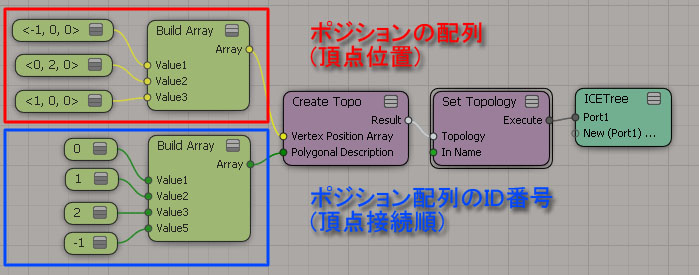
まずは、メッシュの頂点位置情報を3Dベクターの配列として定義する必要があります。

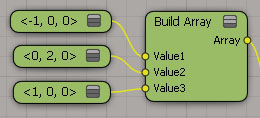
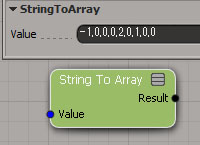
3Dベクターの配列を作成するアプローチは複数存在します。サンプル画像のように、たくさんの3Dベクター情報を“Build Array”ノードのインプットとして利用も出来ます。あるいは、スクリプトを利用してテキストファイルから頂点情報を読み込んで“String To Array”ノードで文字列を配列に利用することも出来るでしょう。

皆様が理想とする形で読み込んだ3Dベクターの配列を頂点位置情報として利用することで自由にメッシュを作成出来るのです。



“Create Topo”ノードに頂点位置情報を与えたら、続いて、それらの頂点がどのような順番で接続すべきかを指定する必要があります。この接続順序が、Polygonal Descriptionを決定するのです。

頂点として利用したい位置情報の配列インデックスからなる整数値の配列がPolygonal Descriptionを示します。与えられた点と点を接続していくことをイメージしていただくと分かりやすいかもしれません。

この例では、インプットの頂点位置情報とポリゴンの描画におけるそれらのエントリーの対応を矢印で示しています。



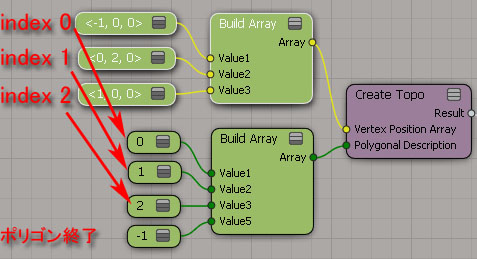
最後のマイナスの値（一番下の-1）についての説明が不足していました。これは、“Create Topo”ノードに対してポリゴンの描画が完了したことを伝えるためのノードです。

実際には、-1でなくとも、どんなマイナスの値でも問題ありません。このマイナスの値が無い場合にはポリゴンのPolygonal Descriptionが完結せずにICEによってポリゴンは作成されません。文章の最後の句点のようなものだと考えてください。

もう一度まとめると、3つの位置情報のインプットがあり、Polygonal Descriptionは4つのエントリーが存在します。3つのポジションID、そして処理を完了するための一つのマイナスの値です。

さて、第一回の記事ではトポロジーに関する理解を深め、シンプルなポリゴンの作成を行いました。次回はさらにポリゴン描画と法線の関係性についてお話し致します。