チュートリアル / Psyop:Todd Akitaと歩むICEマスターへの道のり
第4回:サイン・コサインの基礎
- コラム
- スクリプト・API
- チュートリアル
- 上級者
- 映画・TV
サイン・コサインの視覚化
今回は、サイン・コサインの基礎について解説を行っていきます。まずは、三角形の辺の長さと、内角の関係性について理解を深めることから始めます。それには、三角形の斜辺が上向きになるにつれて側辺の長さの比率が、どう変化をするかを観察するのが良いでしょう。図のように、三角形の斜辺が真上を向くまで、反時計回りに等間隔で回転を行います。
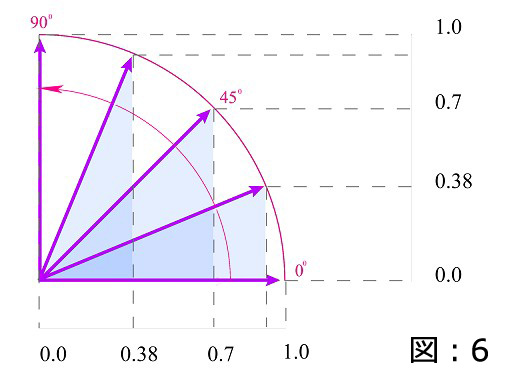
上方向への回転が進むにつれて、画像で陰影がついている下部X軸方面の長さは徐々に短くなっていきます。そして、45度の角度に達した時では、X軸におけるベクトルの投影(陰影)の長さが 0.7 であることに気づかれたでしょうか。(図:6)
回転角度と長さの関係を投影して観察すると、その数値の変化はリニアな動きでないことがわかります。Y軸の垂直方向に投影したエッジの長さをグラフ化すると、-1から1の間でスムースな周期を描くカーブが表れるのです。(図:7)
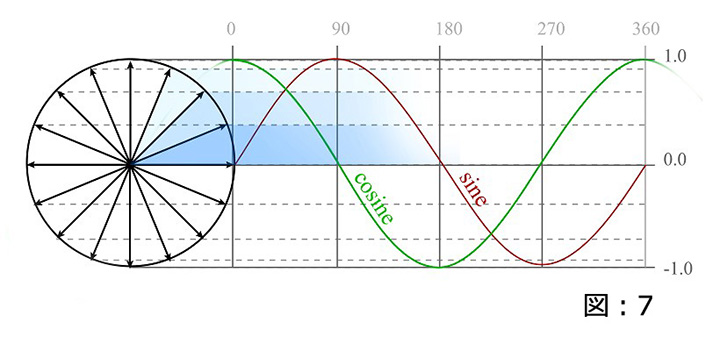
このグラフからサインとコサインは、360度(2πラジアン)間隔の周期的(サイクルと繰り返しを意味します)な動きであることが分かります。また、サインとコサインのカーブの形は似通っていて、違いは90度オフセットしていることだけであることも確認が出来るでしょう。(図:7)
以下の図では、基準となる円に内接するよう三角形を配置しています。そして、サインとコサインを用いてX軸、Y軸方向に沿ってコンスタントに増加する回転値をプロットして図式化しました。(図:8)
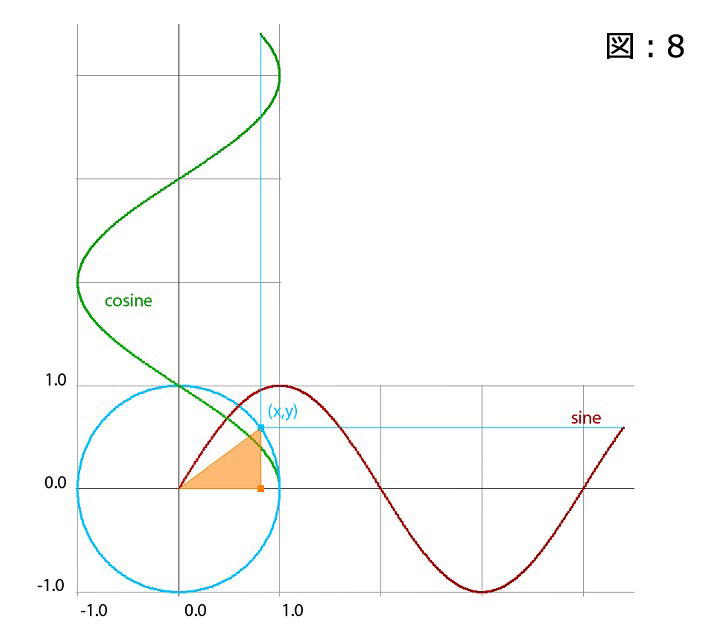
コサイン関数の描く曲線は、円に内接する三角形のエッジ部分の X 座標が基準であることが分かります。同様に、サイン関数の描く曲線は、円に内接する三角形のエッジ部分のY 座標が基準であることが分かります。(図:8)
内角が0から360度に増加するにともない、X軸方向のコサインとY軸方向のサインの交差するポイント群は完全な円を描きます。(図:9)
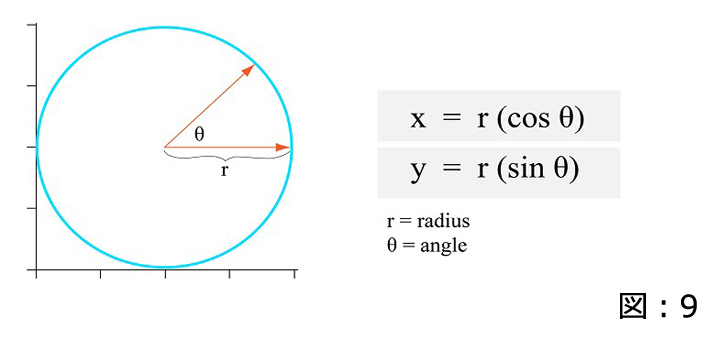
円のパラメトリック方程式は次のとおりです:
x = r * cos(angle)
y = r * sin(angle)
“r”は、円の半径であり、”angle(角度)”は、0から360の数値の変化を指します。(図:9)
三角法の応用
サインやコサインを利用することで完全な円、あるいは部分的な円を表現出来ることがわかりました。これを応用することで、軸の回転を再現することも可能です。
次の例では、サインとコサインを用いてジオメトリの頂点情報を加工しています。XとYコンポーネントに対し2次元的(XY平面でのZ軸)な回転を行なっている例です。(図:10)
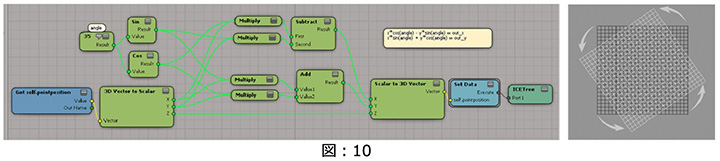
先ほどの例は、XY平面での2次元的な回転でした。XYZに対して平面回転を連続適用することで、3次元空間での回転を表現することも容易です。
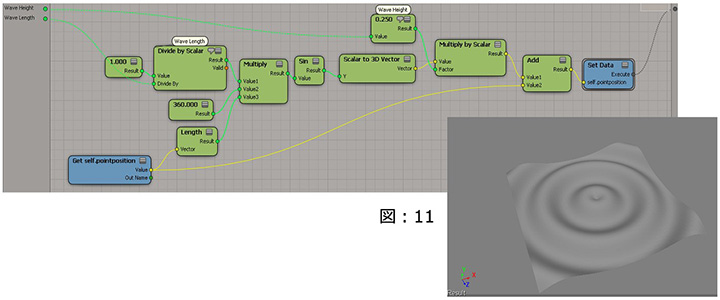
続いて、サインとコサイン関数を用いて、波のように振動する動きを作り出す例を紹介します。サイン・コサインは、周期的な動きで繰り返し・サイクルを表現が出来るため、プロシージャル テクスチャやプロシージャルなデフォーメーションでは頻繁に利用されているテクニックです。(図:11)
また、三角法の逆三角関数を利用して 長方形/極 コーディネートの変換を行うことも可能なのです。ここでは、 ArcTangent を使って、花の中心から長方形のX/Y ポジションへと、ピクセル(パーティクル)を用い角度(距離)に変換してマッピングを行なっています。(図:12)
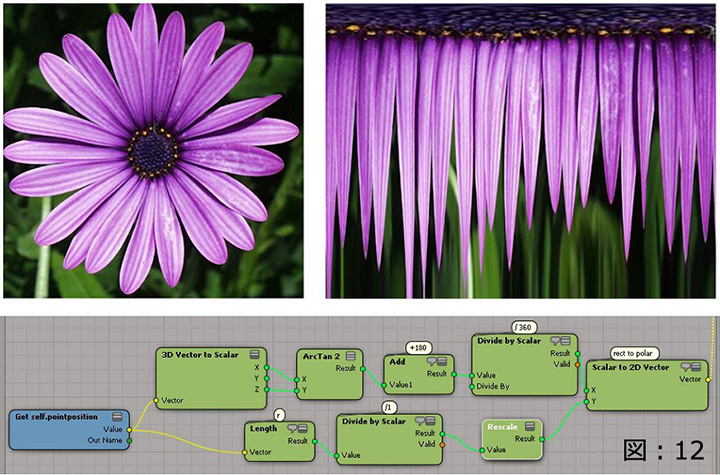
ICEツリーを注意深く見ると、標準のArcTanノードではなく、ArcTan2ノードを利用していることに気付かれたでしょうか?これは、ArcTan2が完全な円(-180度から180度)の角度の範囲を返すからです。一方、ArcTanのほうは、半円(-90度から90度)の角度の範囲を返します。
サイン、コサインとタンジェント、そして逆関数は、辺の長さの比率や三角形の内角の情報を導き出すものです。さて、皆さんは、三角法がもっと他の表現にも応用出来ると感じられたでしょうか?
直面するタスクで、どのように基礎を応用するかは皆さんのアイデア次第です。例えば、サイン・コサインの概念は、次のような実際のPsyopが手がけるプロジェクトでも使用されています。
LG "Something's Lurking" from Psyop on Vimeo.
British Gas "Flotilla" from Psyop on Vimeo.
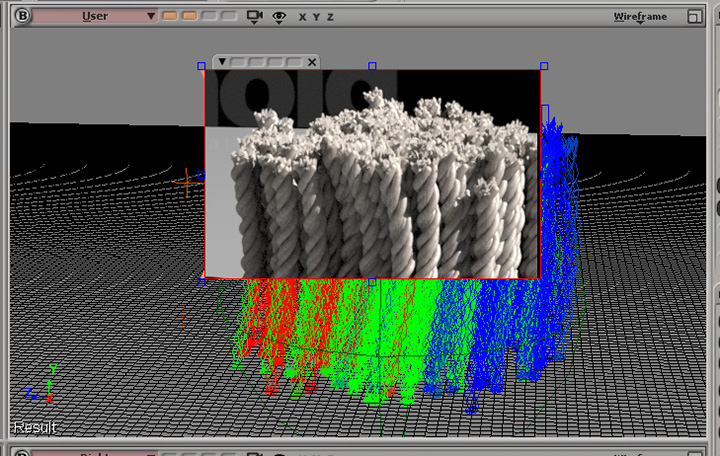
LGプロジェクトのツイストしたカーペット繊維、そして、British Gasプロジェクトのカーリーなアフロヘアは、サイン・コサインの波形がベースとなっていることに気付かれたでしょうか?数学の基礎を理解することで、こういったユニークな表現にも応用が出来るのです。
次回は、ベクトルについての理解を深めて行きたいと考えています。



