チュートリアル / Psyop：Todd Akitaと歩むICEマスターへの道のり
第5回：ベクトルの基礎

ベクトルをあらためて理解する

これまでのレッスンではピタゴラスの定理を使って直線の距離が求められることや、XYZコンポーネントを直角三角形の辺として扱いベクトル情報が求められるといったことを学んできました。（図：13）



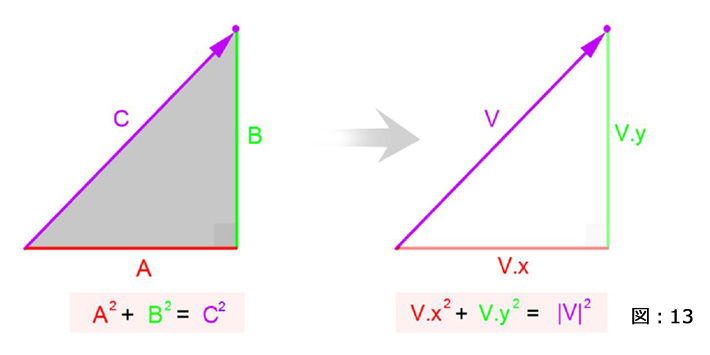
ベクトルの基礎について、今回は解説していきたいと思います。
ベクトルのひとつの捉え方として、開始点と終了点をもつ矢印を考えると良いかもしれません。
この例では、ベクトルの開始点が空間の頂点で、ベクトルの終了点は、原点である (0, 0, 0) です。

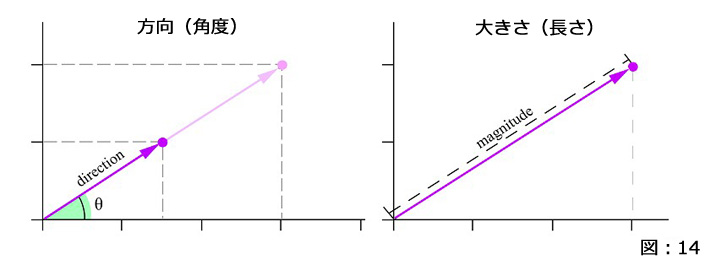
ベクトルには、興味深い2つの独立した要素が存在します。方向（角度）と大きさ（長さ）という要素です。（図：14）

ベクトル加算

2 つのベクトル要素を加算することは、これらのベクトルの先頭と終端をつなげるということです。 （図：15）



ベクトル加算は可換(かかん)です。つまり、演算の順序を変えても結果は変わらないという意味です。

もっと、シンプルに言い換えると、A+B = B+A ということです。

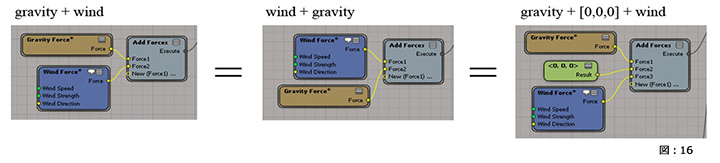
例えば、パーティクルシミュレーション（重力+ウィンド）を加算した際に、加算の順序（ウィンド+重力）が異なっても最終結果は同じとなると言い換えたほうが分かりやすいでしょうか。（図：16）

ベクトル減算

ベクトル同士を加算出来るように、同様に減算も行えます。
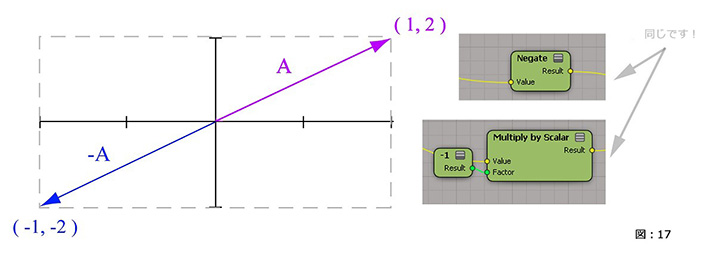
ベクトルの減算は、逆ベクトルの加算、あるいはベクトルを反転するのと同じです。

ベクトルの反転とは、要素を -1 で掛け算することと同様です。
反転すると、新しいベクトル(逆ベクトル)は反対の方向を指すようになりますが、その長さは変わりません。（図：17）



ベクトル減算は、ある点から別の点への相対距離を表す必要があるときによく使用されます。（図：18）



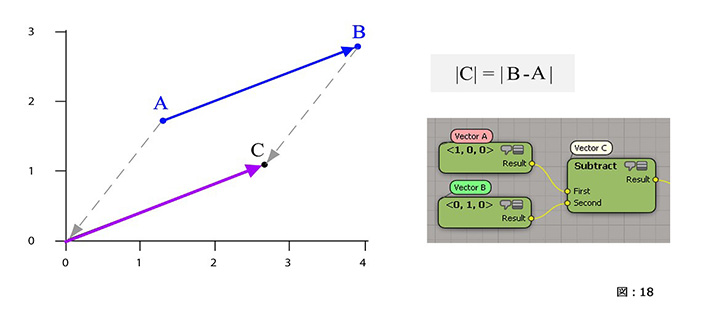
例えば、AとBの相対距離を求めたい場合、B の位置から A の位置を引くことでベクトル C が求められます。
これは、この 2 点間の距離にあたります。

つまり、A と B のペアを A の逆ベクトルでオフセットし A を原点に配置した状態がベクトル C とも言えます。

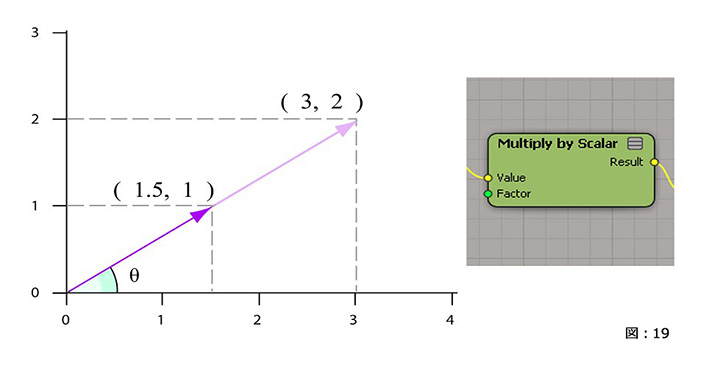
ベクトル / スカラー 乗算（ベクトルのスケール）

ベクトルは、それぞれの要素にスケーリング係数を掛けることでスケーリングが可能です。
ベクトルをスケーリングすると、ベクトルの大きさ（つまり長さ）が変わりますが、方向については変わりません。（図：19）

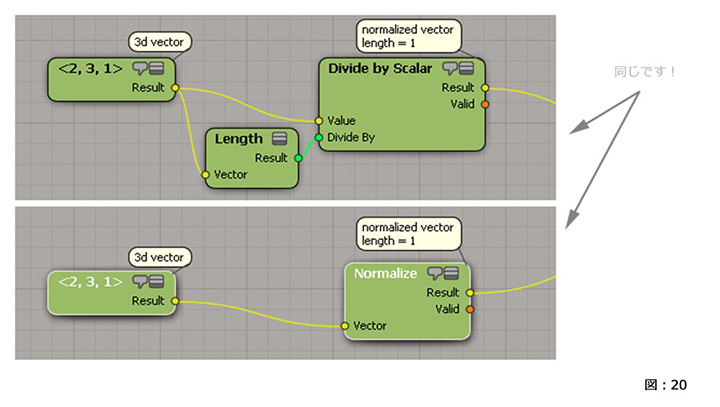
ベクトル / スカラー 除算（ベクトルの正規化）

ベクトルの各要素を長さで割ると、算出されるベクトルの長さは 1.0 になります。
長さ 1.0 の任意のベクトルを単位ベクトルといいます。このようなベクトルを正規化ベクトルと呼びます。（図：20）

ベクトルとベクトルの乗算

ベクトル同士を掛け合わせる方法は 、内積と外積という2つが存在します。

一つ目の内積（またはスカラー積）による乗算結果はスカラー値です。
内積は、演算順序は問題にならない可換です。

二つ目の外積（またはベクトル積）による乗算結果では 、2 つのベクトルの積としてベクトル量が求められます。
外積は、可換ではないために演算順序には気をつける必要があります。


今回は様々なベクトルの計算タイプや可換について図を用いて解説を行いました。
次回のレッスンでは、内積と外積についてより具体的に掘り下げていきたいと思います。