チュートリアル / Bifrost for Maya Rigging Challenge~一歩先のリグ・アニメーションに挑戦~
第2回:多関節ロボットアームのリグ
- Maya
- アニメ
- キャラクター・リグ
- ゲーム
- コラム
- シミュレーション
- チュートリアル
- 上級者
- 中級者
- 映画・TV
みなさんこんにちは。
本コラムではMayaのプラグイン"Bifrost"を使って、リグ、アニメーション、物理シミュレーションなどの観点から作成例を紹介していきます。今回は、前回に引き続きMaya標準ノードでは組めないものとして反復計算が必要な「多関節 (3関節以上)のIK」を作りたいと思います。
成果物は以下のGIFの通りです。こちらを組んでいきます。
【環境】
・Windows 11
・Maya 2025.1
・Bifrost 2.10.0.0
状況の確認
まずはこちらをご確認ください。関節数が4つほどのロボットアームにジョイントが入っています。各関節は捻りと曲げの2軸に分解されていますので、それぞれ2ジョイントで構成されておりエンドを含めてアーム部分は計9ジョイントあります。モデル的に重要なのは先端部分なのでこれを“IKゴールの位置だけで手軽に制御”したいです。
通常のIKソルバ(RPSolverなど)を根本から先端に入れるのは上手くいく気はしません。とはいえ2セクションずつ分解してIKを複数適用するのも今回はちょっと嫌です。SplineIKはゴール位置を明確にコントロールできないので却下になります。motionPathを使ったリグならゴール位置をコントロール出来ますが伸縮を許してしまうことになるのでデザイン的にナシです。2軸に分解された関節も対応に悩みます。
そこで、任意の関節数で使える反復法によるIKアルゴリズムを実装してみよう!というのが今回の試みになります。
FABRIK
3関節以上のIKアルゴリズムは何種類かありますが、今回は角度制限や分岐にも対応できて実装が比較的簡単なFABRIK(*1)を採用してみます。FABRIKのアルゴリズムは次の図のようになります。手順が多く初見は混乱しやすいですが、実際は非常に単純な計算の繰り返しです。
まずtargetに末端の点を移動してからp(n-1)、p(n-2)、p(n-3)、、、p1へ以下の計算式①の処理を繰り返します。このフェーズをForward Reachingと呼びます。その後、逆に根本の点を元の位置に戻すところから始めてp2、p3、p4、、、pnと以下の計算式②の処理を繰り返します。こちらはBackward Reachingと呼びます。式の形が似ているのでなんとなく分かるかと思いますが、ForwardとBackwardは向きが逆なだけで処理内容はほぼ同じ「1つ前の点との間の距離を元のまま保つように点を移動する」になっています。
ではこちらをBifrostグラフで組んでみます。FABRIKで取り扱うのはただの点ですので、まずはジョイントの階層や回転は無視して位置(float3)の配列(Array)を入出力とします。今回は効率よく配列を使い関節数の変更に耐えうる構造にしていきます。IKゴールを基点に配列を逆順に処理するのがForward、その後、根元の位置を基点に配列を先頭から順に処理するのがBackwardです。
配列の中身をひとつひとつ取り出して処理を行うにはiterateを使います。iterateへ配列を入力し、イテレーション内でget_from_arrayで要素を取り出してしかるべき処理を行ったら、set_in_arrayで配列に値を戻し配列を出力します。この場合は出力ポートはStateに設定しておきます(*2)。こうすることで、配列の2番目の処理時(反復の2周目)には配列の1番目の要素はすでに更新されている状態になります。
*2) シンプルな処理であれば出力を単一の値にしてポートをIteration Targetに設定する方法もありますが、今回のケースでは配列の要素を次々に更新しながら進めていく必要があるため、Stateポートを使用します。
結果は以下のようになりました。分かりやすいようにpoint_scopeを入れてあります。入力点が白の⚪︎、Forward後が赤の⚪︎、Backward後が緑の⚫︎です。
もうほぼ出来ているようなものですが、全体の反復計算をしていないので末端がIKゴールからたびたび外れています。最後に、ForwardからBackwardの部分をさらにiterateで括り、位置配列をStateポートにします。すると上記手順がMax Iterations回反復計算され、結果が収束していきます。
角度制限
前項で「ゴール位置のみで制御可能な多関節IK」まで完成しましたが、実際のjointに適用するには少し問題があります。
・関節可動域が360°なので曲がりすぎる
・IKゴールのコントローラでアーム先端付近の向きを制御したい
角度制限は、ForwardおよびBackward Reachingにて点を移動する時に『基準となるベクトルとの間の角度が指定角度を超えていたら、制限内に戻す』という工程を挟めば導入できます。制限範囲はコーン状です。
2つのベクトルv1、v2の間の角度θを確認し、指定角度θmaxを超えていたら超えた分だけv2をv1方向に回転させて制限内に戻します。この時の回転軸aはv1とv2に垂直なベクトルです。
あるベクトルを軸に別のベクトルを指定角度だけ回転させるには“ロドリゲスの回転公式”(式①)が使えます。ただし、aとv2は直交しているので内積a・v2は必ずゼロになり、今回必要としている角度制限の式においては式②のように簡略化することができます。
ではBifrostグラフに移ります。コーンを描画する機能は現状のBifrostには無さそうなので自作しています。この場での解説は割愛しますがサンプルデータに含まれていますので気になる方はご確認ください。
ではこちらをFABRIKのグラフに追加します。Forward、Backwardともに2番目から最後の点までが角度制限の対象です。基準軸は、2番目のみ指定したベクトルを使い、3番目以降は1つ前と2つ前の点からベクトルを得ます。
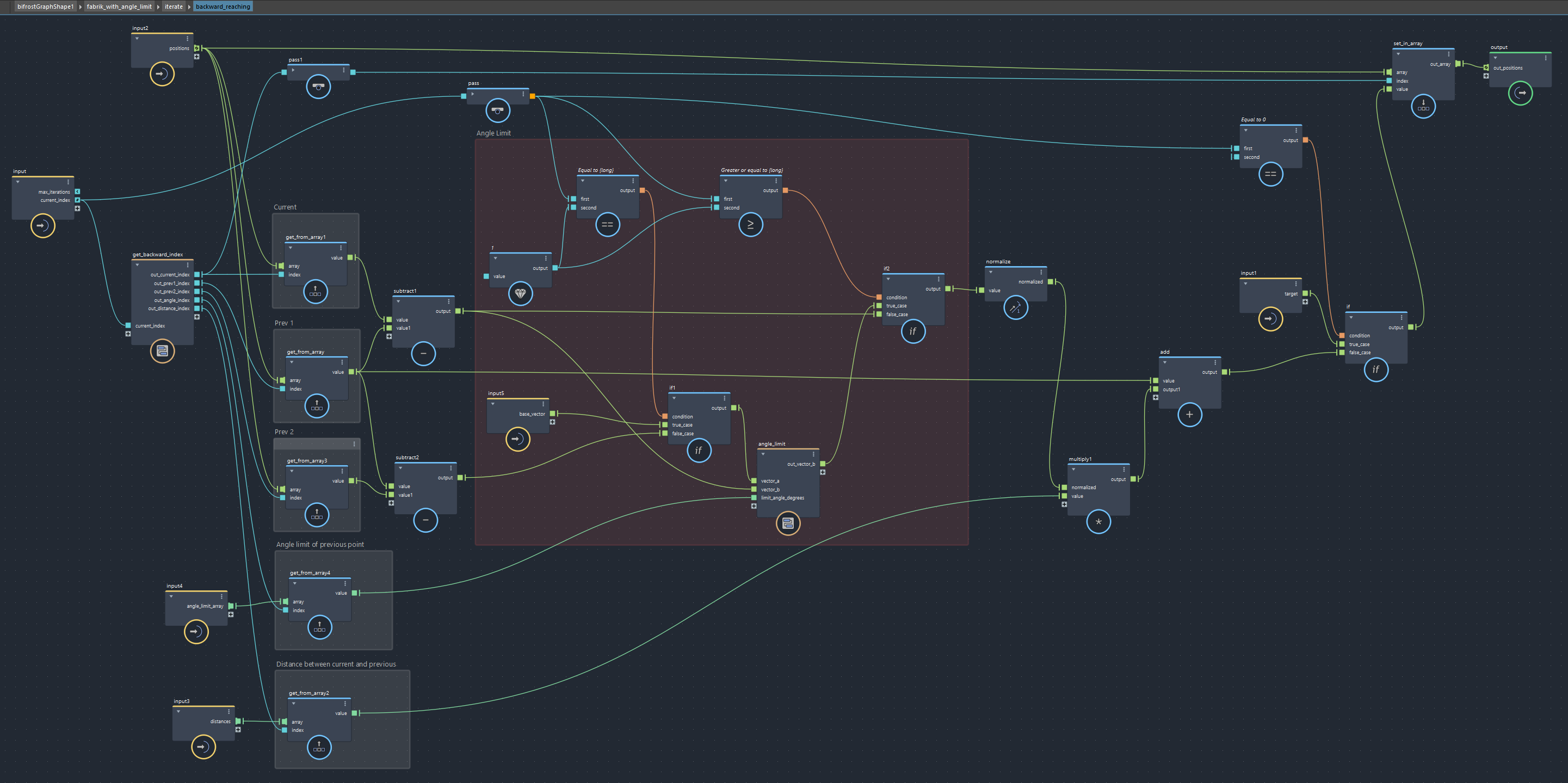
これでIKの動きは完成しました!ちなみに、エンド付近に厳しい角度制限があるとデッドロック状態(*3)に陥りやすくなるので注意が必要です。今回は対処はせずに進めます。
*3) Extending FABRIK with model constraints デッドロックについてはこちらの論文の「5.4. Dealing with the Deadlock Situation」で解説されています。
ベクトルを2軸(捻り・曲げ)に分解
前項までは全てベクトルのみで制御していましたので、ジョイントに適用できるように回転に変換していきたいと思います。今回のモデルは"捻りの下階層に曲げ"の構造なのでこれらをベクトルから分解して取得します。
以下は更新前と後の2つのベクトルa、bから捻りと曲げを得る図です。この場合はX軸が捻り軸なので、2つのベクトルをYZ平面に投影し、その間の角度から捻り成分が得られそうです。また、X軸に平行なベクトルxとaの間の角度、xとbの間の角度をそれぞれ求め、差分を求めれば曲げ成分が得られます。
Bifrostグラフは以下の通りです。それぞれのベクトルは親の空間内で考える必要があるため、まず初めに親の逆行列で変換してから角度の計算をします。
ベクトルから捻りと曲げへの変換が出来ました!ようやく冒頭のロボットアームへ適用できます!
ここまでの結果を元にリグを完成させる
最後に、これまでの結果を合わせてグラフを完成させます。角度制限ありのFABRIKでIK制御→捻り曲げ変換です。かなり複雑なグラフに見えますが、ここまでで解説してきた内容を合わせていくだけになります。
*4) Joint Orientは変動する値ではないのでこの状態から接続を切断し、値がセットされているだけの状態にしたほうが、Cycleがなくなりパフォーマンスが上がる場合があります。
これで完成です!
前回に引き続きベクトル演算ノードとiterateを使い、今回は多関節IKを作成してみました。反復計算が使えるようになるとMaya標準ノードよりも手法の選択肢が広がります。最後の回転に変換するところは少し難易度が高いかもしれませんが、無理に変換せずワールド位置座標をMayaへ出力しAimコンストレイントなどでなんとかするという手もあります。もしすべての関節がボール&ソケットだったらもっと簡単になりますね。
また次回をお楽しみに!
今回のまとめ
・反復計算ができると多関節IKのアルゴリズムを実装できる
・iterateは配列の中身をひとつずつ取り出して処理する用途でも使える
・FABRIKは単純なベクトル計算だけなので応用やアレンジがしやすい
・ベクトルは最後に回転へ変換する
















































